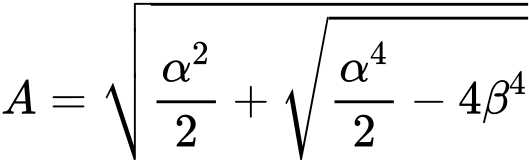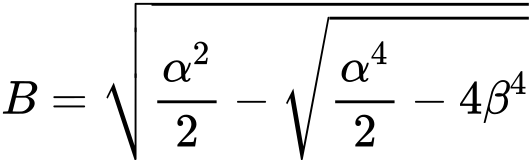Metoda geometryczna (Eulera)
Grunt w otoczeniu mikropala jest w programie reprezentowany za pomocą modułu reakcji gruntu (podłoża) Ep (stała Winklera k) zdefiniowanego przez użytkownika w ramce "Analiza przekroju". Model konstrukcji przedstawiono na rysunku.
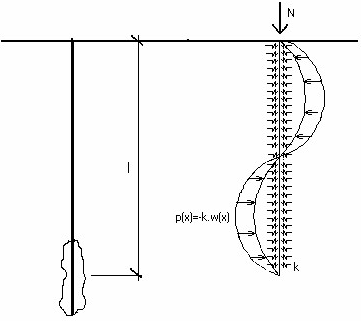 Model konstrukcji
Model konstrukcji
W przypadku mikropala pod obciążeniem ściskającym oczekiwane jest wystąpienie zmiennej liczby pół-fal, w zależności od geometrii i sztywności, odpowiednio: konstrukcji i otaczającego gruntu. Rozwiązanie w tym przypadku pochodzi z równania zginania belki prostej.
![]()
Po przekształceniach, równanie zginania można wyrazić w następujący sposób:
| |
gdzie: | |
| |
| |
| |
|
Stałe całkowania C1-C4 określane są na podstawie czterech warunków brzegowych zależnie od przyjętego sposobu podparcia punktów końcowych.
Siła krytyczna Ncr wyznaczana jest z następującego wzoru [1]:
![]()
gdzie: | Ei | - | moduł sprężystości przekroju idealnego |
Ii | - | moment bezwładności przekroju idealnego | |
lp | - | długość efektywna mikropala (długość wolna + 1/2 długości buławy) | |
Ep | - | ||
n | - | liczba pół-fal |
Siła krytyczna Ncr przyjmowana jest jako minimum funkcji (1). Jest to osiągane dla długości pół-fali wynoszącej:
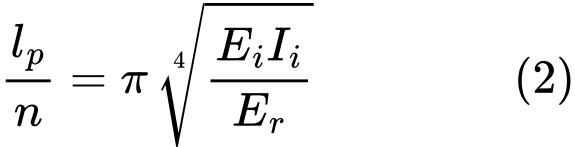
Liczba pół-fal n wyznaczana jest na podstawie wzoru (2):
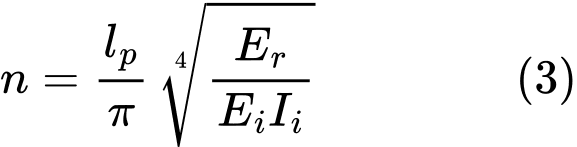
W przypadku, gdy część mikropala wyniesiona jest ponad powierzchnię terenu (wyniesienie głowicy mikropala nad teren), zredukowane wartości n oraz Er wyznaczane są w sposób następujący:
![]()
![]()
gdzie: | lv | - | długość mikropala ponad terenem |
W przypadku przyjęcia warunku przegub-przegub, zastosowanie ma następujące równanie:
![]()
W przypadku przyjęcia warunku przegub-utwierdzenie, zastosowanie ma następujące równanie:
![]()
Literatura:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936