Model Hardening soil
Model Hardening soil opracowany przez Schanz et al. [1] ma zastosowanie do modelowania szerokiego zakresu gruntów "miękkich". Model ten łączy dwa mechanizmy wzmocnienia. Mechanizm wzmocnienia przy ścinaniu napędza ewolucję odkształceń plastycznych wywołanych przez składowe naprężenia dewiatorowego, podczas gdy mechanizm w ściskaniu staje się aktywny w ściskającym trybie obciążenia, np. w edometrze lub przy ściskaniu izotropowym. Mechanizm wzmocnienia przy ścinaniu objawia się stopniową ewolucją powierzchni plastyczności ścinania fsHS w zależności od aktualnej wartości równoważnego dewiatorycznego odkształcenia plastycznego κs (lub γps).
Proces wzmocnienia (rozszerzenie powierzchni plastyczności) jest połączony z ewolucją zmobilizowanego kąta tarcia wewnętrznego φm i kończy się osiągnięciem granicznej powierzchni plastyczności ścinania fsMN. W programie GEO5 MES ta funkcja plastyczności jest przedstawiona w postaci kryterium zniszczenia Matsuoka-Nakai, będącego funkcją wartości szczytowych parametrów wytrzymałości na ścinanie, spójności c i kąta tarcia wewnętrznego φ. Rzut powierzchni plastyczności na płaszczyznę dewiatorową jest zatem gładką krzywą wypukłą przechodzącą przez wszystkie wierzchołki modelu Mohra-Coulomba. Konsekwencją wzmocnienia ściskającego jest ewolucja powierzchni plastyczności cap fcHS w zależności od ewolucji ciśnienia prekonsolidacji pc. Podobne sformułowanie opracowane w odniesieniu do niezmienniczych miar naprężeń przedstawiono również w [2].
Graficzne przedstawienie obydwu powierzchni plastyczności jest widoczne na poniższym rysunku. W celu zilustrowania przedstawiono stopniową ewolucję powierzchni plastyczności ścinania, widoczną z rzutu powierzchni plastyczności na płaszczyznę południkową. W podobny sposób zdefiniowano model Soft soil, który jednak uwzględnia jedynie graniczną powierzchnię ścinania. Wzmocnienie jest zatem ograniczone do powierzchni CAP w ściskaniu.
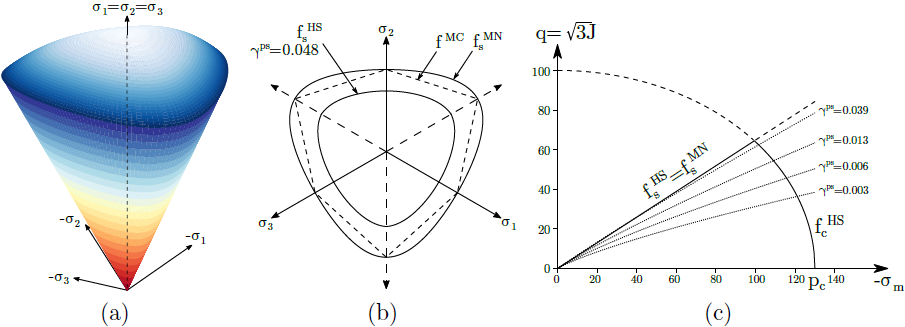 a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) projekcja na płaszczyzny dewiatoryczne i c) płaszczyzny południkowe
a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) projekcja na płaszczyzny dewiatoryczne i c) płaszczyzny południkowe
Sformułowanie powierzchni plastyczności ścinania wynika z założenia, że zależność między naprężeniem dewiatorowym i odkształceniem pionowym ε3 podczas badania trójosiowego z opływem można opisać funkcją hiperboliczną. Odpowiedni wykres naprężenie-odkształcenie przedstawiono na poniższym rysunku, gdzie qa jest wartością asymptotyczną q a qfMC odpowiada wartości q po osiągnięciu powierzchni granicznej, w którym to przypadku obowiązuje: qf = Rfqa, gdzie Rf jest współczynnikiem redukcji. Więcej szczegółów można znaleźć w podręczniku teoretycznym.
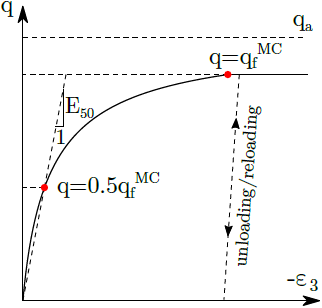 Hiperboliczne prawo naprężenia-odkształcenia
Hiperboliczne prawo naprężenia-odkształcenia
Parametry definiujące model materiałowy Hardening soil podsumowano w poniższej tabeli.
Symbol | Jednostka | Opis | |
| [MPa] | Sieczny moduł sprężystości | |
| [MPa] | Moduł odciążenie/dociążenie | |
| [-] | Współczynnik Poissona | |
| [kPa] | Średnie naprężenie odniesienia | |
| [-] | Wykładnik prawa potęgowego sztywności | |
| [kPa] | Wartość graniczna naprężenia średniego zapewniająca sztywność różną od zera | |
| [kN/m3] | Ciężar objętościowy | |
| [-] | Początkowy wskaźnik porowatości odpowiadający stanowi na koniec 1. fazy obliczeń | |
| [-] | Współczynnik uszkodzenia | |
| [kPa] | Maksymalna spójność efektywna | |
| [°] | Maksymalny efektywny kąt tarcia wewnętrznego | |
| [°] | Kąt dylatancji | |
| [kN/m3] | Ciężar objętościowy | |
| [-] | Współczynnik parcia spoczynkowego gruntu normalnie skonsolidowanego | |
| [MPa] | Styczny moduł edometryczny | |
| [kPa] | Pionowe naprężenie odniesienia do określenia | |
| [-] | Maksymalny współczynnik porowatości do zakończenia dylatancji (przy ograniczeniu dylatacji) | |
| [-] | Wskaźnik prekonsolidacji | |
| [kPa] | Ciśnienie początkowe nadkładu | |
| [1/K] | Współczynnik rozszerzalności cieplnej (w przypadku uwzględnienia wpływu temperatury) | |
| [-] | Parametr definiujący kształt powierzchni CAP w ściskaniu | |
| [Pa] | Moduł wzmocnienia (nie zdefiniowany) | |
| [kPa] | Ciśnienie prekonsolidacji | |
| [°] | Kąt tarcia stanu krytycznego (nie zdefiniowany) | |
| [°] | Zmobilizowany kąt tarcia wewnętrznego (nie zdefiniowany) | |
| [°] | Zmobilizowany kąt dylatancji (nie zdefiniowany) |
Sieczny moduł sprężystości Eip,ref można przybliżyć za pomocą modułu sprężystości E50p,ref w sposób następujący:
![]()
gdzie wskaźnik (p,ref) reprezentuje wartość odniesienia modułu odnoszącą się do pewnej wartości odniesienia efektywnego naprężenia średniego σmref. Ogólnie rzecz biorąc, model zakłada ewolucję modułu sprężystości w funkcji aktualnego średniego naprężenia w postaci:
![]()
Należy zwrócić uwagę, że ta formuła różni się od tej stosowanej na przykład w publikacjach [1] i [2], gdzie ewolucja sztywności zależy od minimalnego naprężenia głównego, w tym przypadku σ1. Należy to uwzględnić przy przyjmowaniu parametrów skalibrowanych dla innego oprogramowania inżynierskiego w programie GEO5 MES. Potencjalną opcją jest użycie zmodyfikowanego zestawu parametrów, który zapewnia rozsądne dopasowanie symulacji dostarczanych przez poszczególne programy. W tym celu prosta regresja liniowa wydaje się wystarczająca do dostosowania parametrów Eurp,ref i mp. Ilustrujący przykład tego konkretnego podejścia przedstawiono na poniższym rysunku.
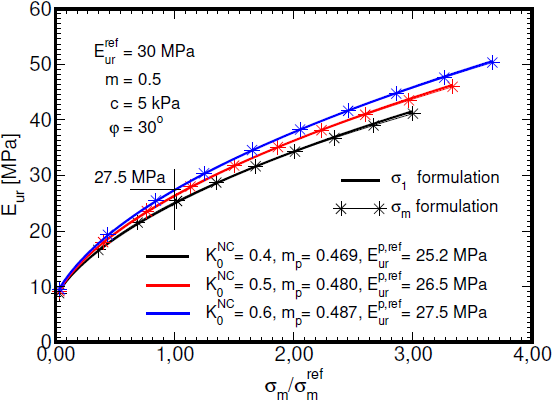 Określanie zależności modułu odciążenie/dociążenie Eur od naprężenia średniego σm z wykorzystaniem regresji liniowej
Określanie zależności modułu odciążenie/dociążenie Eur od naprężenia średniego σm z wykorzystaniem regresji liniowej
Zmodyfikowane parametry E50p,ref(Eip,ref) i Rf można uzyskać później w etapie optymalizacji, porównując symulacje numeryczne badania ściskania trójosiowego, wykorzystując wcześniej określone parametry Eurp,ref i mp.
Więcej szczegółów można znaleźć w podręczniku teoretycznym. Jednakże zdecydowanie zaleca się kalibrację konkretnych parametrów modelu, powiązanych z konkretnym wdrożeniem, na podstawie dostarczonych pomiarów laboratoryjnych, np. przy użyciu oprogramowania kalibracyjnego ExCalibre.
Ograniczenie ściskania CAP fcHS charakteryzowane jest za pomocą parametru M określającego jego kształt i moduł wzmocnienia H zapewniając przyrost ciśnienia prekonsolidacji Δpc w odniesieniu do przyrostu objętościowego odkształcenia Δεvpl. Moduł wzmocnienia H wyznaczany jest w sposób następujący
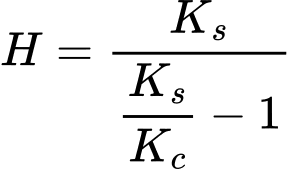
gdzie Kc, Ks są modułami objętościowymi przy pierotnym obciążeniu i odciążeniu, odpowiednio. Więcej szczegółów można przeczytać w podręczniku teoretycznym. Parametry ![]() mogą być wprowadzane bezpośrednio lub określane automatycznie na podstawie wartości współczynnika parcia spoczynkowego gruntów normalnie skonsolidowanych K0NC i modułu edometrycznego Eoedref. Osiąga się to poprzez numeryczną optymalizację laboratoryjnego badania edometrycznego. Celem jest określenie parametrów modelu M, H tak, aby numerycznie wyznaczony moduł edometryczny odpowiadał modułowi określonemu dla danej wartości K0NC jak pokazano na poniższym rysunku. Naprężenie średnie σm* oraz równoważne naprężenie dewiatoryczne J* są wyznaczane za pomocą
mogą być wprowadzane bezpośrednio lub określane automatycznie na podstawie wartości współczynnika parcia spoczynkowego gruntów normalnie skonsolidowanych K0NC i modułu edometrycznego Eoedref. Osiąga się to poprzez numeryczną optymalizację laboratoryjnego badania edometrycznego. Celem jest określenie parametrów modelu M, H tak, aby numerycznie wyznaczony moduł edometryczny odpowiadał modułowi określonemu dla danej wartości K0NC jak pokazano na poniższym rysunku. Naprężenie średnie σm* oraz równoważne naprężenie dewiatoryczne J* są wyznaczane za pomocą
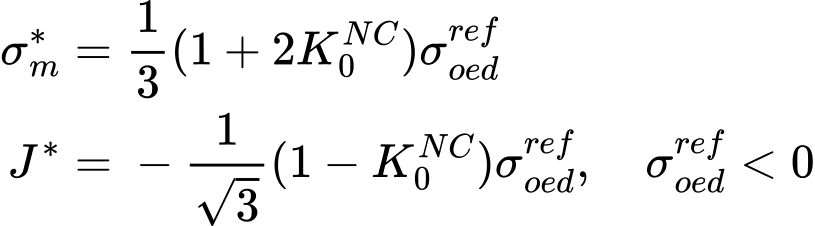
Więcej szczegółów można znaleźć w przewodniku teoretycznym.
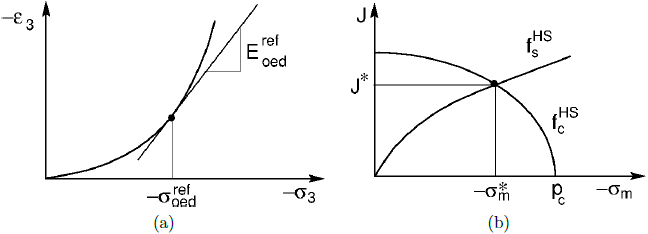 a) graficzna reprezentacja referencyjnego modułu edometrycznego Eoedref w punkcie o określonym σoedref, b) aktualne naprężenie na końcu etapu optymalizacji związane z σoedref
a) graficzna reprezentacja referencyjnego modułu edometrycznego Eoedref w punkcie o określonym σoedref, b) aktualne naprężenie na końcu etapu optymalizacji związane z σoedref
Model Hardening soil umożliwia modelowanie dylatancji gruntu (rozwój dodatnich objętościowych odkształceń plastycznych podczas plastycznego ścinania) poprzez wprowadzenie kąta dylatancji ψ. Rozwój odkształceń plastycznych napędzany jest przez potencjał plastyczny gsHS. Definicja potencjału plastycznego jest zasadniczo identyczna z tą przyjętą dla modelu Druckera-Pragera. Jedyną różnicą jest definicja nachylenia potencjału plastycznego Mψ, który teraz zależy od aktualnej wartości zmobilizowanego kąta tarcia wewnętrznego ψm. Odpowiednie równanie ewolucji tworzy się podobnie jak w modelu zmodyfikowanym Mohra-Coulomba, na bazie teorii dylatancji Rowe'a.
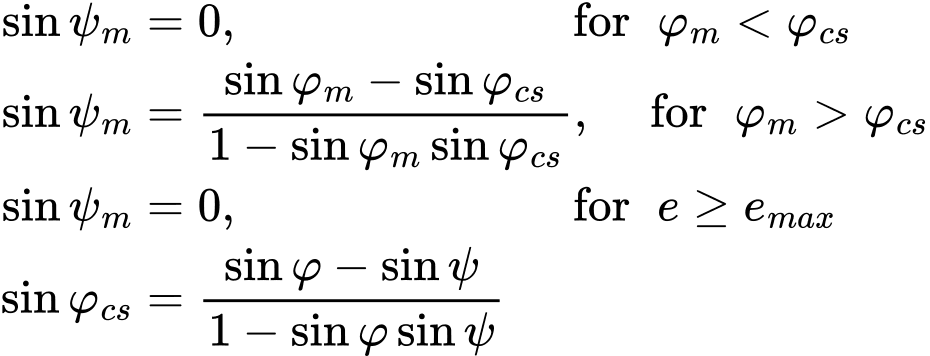
gdzie φ, φm, φcs, ψ są maksymalnym kątem tarcia wewnętrznego, zmobilizowanym kątem tarcia wewnętrznego, kątem tarcia stanu krytycznego i maksymalnym kątem dylatancji. Graficzna reprezentacja ewolucji ψm została przedstawiona na poniższym rysunku. Ilustruje również potencjalne odcięcie dylatacji poprzez wprowadzenie maksymalnego wskaźnika porowatości emax, dla którego spodziewane jest osiągnięcie stanu krytycznego ψm = 0.
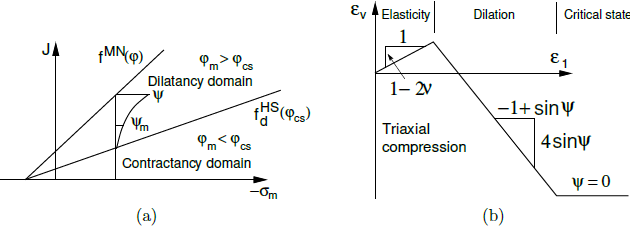 Teoria dylatancji Rowe’a: a) graficzna reprezentacja ewolucji kąta dylatancji zmobilizowanej ψm, b) odcięcie dylatancji
Teoria dylatancji Rowe’a: a) graficzna reprezentacja ewolucji kąta dylatancji zmobilizowanej ψm, b) odcięcie dylatancji
Przypomnijmy, że ewolucja sztywności zależy od aktualnej wartości średniego naprężenia efektywnego σm. Jest to ściśle związane z wyborem początkowego kroku obciążenia, który wymaga bardzo niskich wartości naprężenia początkowego, aby było wystarczająco małe. W celu przyspieszenia konwergencji, przydatne wydaje się wykorzystanie opcji Minimalna liczba iteracji dla pojedynczego kroku obciążenia. Wpływ wielkości początkowego kroku obciążenia na rozwój naprężeń i odkształceń opisano szczegółowo tutaj.
Ważnym krokiem w świetle udanej analizy jest ustalenie początkowych wartości naprężeń prekonsolidacji pcin oraz równoważnego plastycznego odkształcenia dewiatorowego κsin. Obydwa parametry są ustalane w zależności od bieżącego stanu naprężeń w momencie wprowadzenia do analizy modelu Hardening soil, tak aby bieżący stan naprężeń spełniał zarówno funkcję ścinania, jak i funkcję plastyczności CAP. Szczegóły teoretyczne tego zagadnienia przedstawiono tutaj. Można również zapoznać się z opisem modelu zmodyfikowany Cam-clay.
Model pozwala na korygowanie początkowej wartości ciśnienia prekonsolidacji w zależności od oczekiwanego stopnia prekonsolidacji za pomocą parametrów ![]() i
i ![]() . Więcej szczegółów można znaleźć tutaj. Należy pamiętać, że opcja ta jest dostępna tylko w przypadku ustawiania początkowego naprężenia geostatycznego za pomocą procedury K0.
. Więcej szczegółów można znaleźć tutaj. Należy pamiętać, że opcja ta jest dostępna tylko w przypadku ustawiania początkowego naprężenia geostatycznego za pomocą procedury K0.
W przypadku, gdy w analizie wymagane są warunki bez odpływu można procedować wyłącznie za pomocą Typu (1): analiza w naprężeniach efektywnych (cef, φe). Model Hardening soil umożliwia także wykonywanie analizy stateczności. Opcja ta jest jednak dostępna tylko podczas uruchamiania analizy stateczności w obrębie danej fazy budowy. W takim przypadku compression cap jest wyłączana i podobnie ewolucja zmobilizowanego kąta tarcia. W związku z tym, tylko graniczna powierzchnia plastyczności fsMN może stać się aktywna. Zadanie rozwiązuje się poprzez stopniową redukcję maksymalnych wartości parametrów wytrzymałości na ścinanie c, φ w sposób analogiczny jak podano w opisie modelu Druckera-Pragera.
W niniejszym artykule zbadano wydajność modelu w ramach prostych badań laboratoryjnych, w tym wpływ wielkości kroku obciążenia początkowego.
O ile nie ma jednoznacznych dowodów eksperymentalnych na inne wartości, parametry modelu Hardening soil powinny mieścić się w zalecanych zakresach wymienionych w poniższej tabeli.
Symbol | Jednostka | Wartość rekomendowana | |
| [MPa] | (2, 70) | |
| [MPa] |
| |
| [kPa] | 100.0 | |
| [-] | (0.3, 0.9) | |
| [kPa] | 10.0 | |
| [-] | 0.9 | |
| [°] | (16.0, 42.0) | |
| [kPa] | (0.0, 50.0) | |
| [°] |
| |
| [-] | (0.5, 2.5) | |
| [-] | 0,2 | |
| [-] |
| |
| [-] |
| |
| [kPa] | 100.0 | |
| [MPa] |
|
Implementacja modelu materiałowego Hardening Soil w programie GEO5 MES jest szczegółowo opisana w podręczniku teoretycznym.
Literatura:
[1] T. Schanz, P.A. Vermeer, P.G. Bonnier, The hardening soil model: Formulation and verification, Beyond 2000 in Computational Geotechnics, Balkema, Rotterdam. 1999
[2] T. Benz, Small-Strain Stiffness of Soils and its Numerical Consequences, PhD thesis, University of Stuttgart, 2007