Model Soft soil
Oczekuje się, że model Soft soil, pierwotnie zaproponowany w [1], znajdzie zastosowanie w modelowaniu znacząco miękkich gruntów o wysokim stopniu ściśliwości, w przypadku których zastosowanie modelu Hardening soil może okazać się niewystarczające. Podobnie jak model Hardening soil model Soft soil jest reprezentowany przez dwie powierzchnie plastyczności. Powierzchnia plastyczności ścinania bazuje na kryterium zniszczenia Matsuoka-Nakai, a compression cap sformułowano tutaj na podstawie modelu Uogólnionego Cam-clay. Ich rzuty na płaszczyznę dewiatorową są wygładzonymi krzywymi wypukłymi przechodzącymi przez wierzchołki modelu Mohra-Couloma. Graficzną reprezentację modelu przedstawiono na poniższym rysunku.
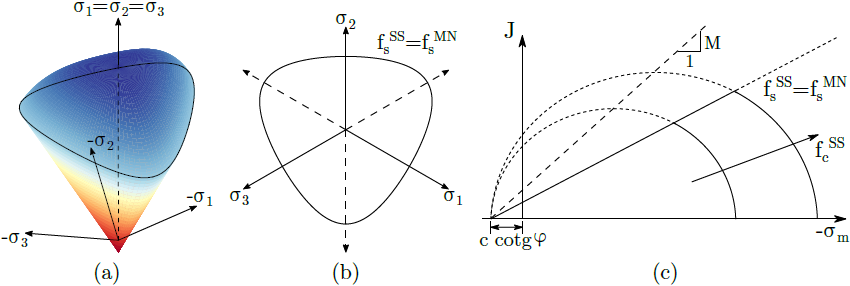a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) projekcja na płaszczyzny dewiatorowe i c) płaszczyzny południkowe
W przeciwieństwie do modelu Uogólnionego Cam-clay nachylenie linii stanu krytycznego M zdefiniowane jest w odniesieniu do współczynnika parcia spoczynkowego dla gruntów normalnie skonsolidowanych K0N oraz parametrów sztywności κ*, λ* w postaci:
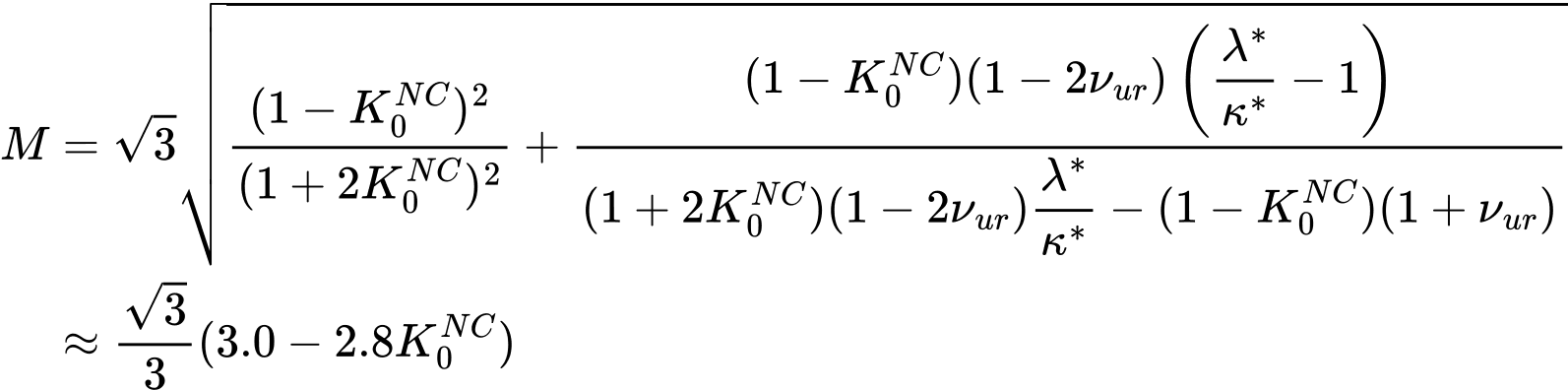
Więcej szczegółów na temat parametrów κ*, λ* podano w opisie modelu Zmodyfikowany Cam-clay. Powodem tej konkretnej definicji jest fakt, że np. wartość parametru M, który w modelu Zmodyfikowany Cam-clay daje prawidłową wartość oporu ścinania, może sugerować wartość K0NC znacznie przekraczającą wartość podaną przez wzór Jaky'ego dla danej wartości kąta tarcia wewnętrznego φ. Więcej szczegółów można znaleźć w [1].
Zakłada się, że powierzchnia plastyczności przy ścinaniu jest zgodna z zachowaniem przedstawionym w sprężysto-idealnie plastycznym modelu materiałowym. Z drugiej strony, compression cap może, w przeciwieństwie do Uogólnionego modelu Cam-clay, ulegać wyłącznie wzmocnieniu. Innymi słowy, ciśnienie prekonsolidacji pc, które napędza ewolucję compression cap, może jedynie wzrastać, patrz również opis modelu Zmodyfikowany Cam-clay. Takie ograniczenie nakłada pewne ograniczenia na dobór parametrów modelu, w szczególności na wartość kąta tarcia wewnętrznego φ. Wymaga to spełnienia następującego warunku.
Ten warunek powinien być spełniony nawet jeśli:
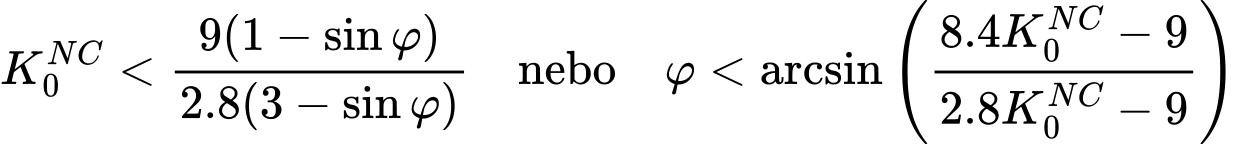
Poniższy rysunek ilustruje graficzną zależność między powierzchnią plastyczności ścinania a compression cap przy ściskaniu dla dwóch różnych wartości K0NC i kilku wartości kąta tarcia wewnętrznego φ dla stałych wartości parametrów κ*, λ*, ν. Oczywiste jest, że dla kombinacji M(K0NC = 0.6) = 0.774 i φ = 40° powyższe warunki nie są spełnione, ponieważ dla pierwszego warunku otrzymujemy φmax = 33.2° < φ = 40°, podczas gdy drugi warunek wymaga nawet φmax = 32.8°, patrz zielony wariant na rysunku (b).
Ponieważ rzuty obydwu powierzchni plastyczności na płaszczyznę południkową zależą od kąta Lode'a przedstawiamy te rysunki dla przypadku ściskania trójosiowego. Szczegóły dotyczące prognozowania osłabienia przez Uogólniony model Cam-Clay można znaleźć w opisie modelu. Zobacz również porównanie prognoz uzyskanych przez Zmodyfikowany model Cam-clay i Uogólniony model Cam-clay dostępne tutaj. Więcej szczegółów można znaleźć w podręczniku teoretycznym.
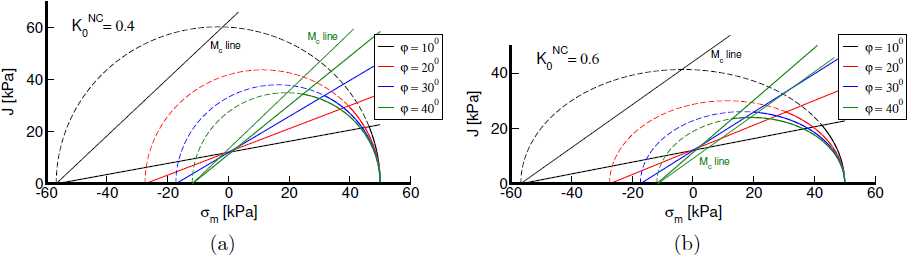Powierzchnie plastyczne przy ściskaniu i ścinaniu: φ i K0NC: a) K0NC =0.4, b) K0NC =0.6
Ewolucja ciśnienia prekonsolidacji pc a także znaczenie poszczególnych parametrów definiujących podstawowe zależności konstytutywne odnoszące się do compression cap, zostały wyjaśnione w opisie modelu Zmodyfikowany Cam-clay. Funkcja potencjału plastycznego, która steruje ewolucją odkształceń plastycznych w obszarze kontrolowanym przez powierzchnię plastyczności ścinania, jest identyczna z tą przyjętą w modelu Druckera-Pragera. Jest ona zatem niezależna od kąta Lode'a. Z drugiej strony, zależy ona od kąta dylatancji ψ (Mψ = Mψ(ψ)). Ogólnie przyjmujemy, że φ ≠ ψ, co odpowiada niestowarzyszonemu prawu płynięcia. Podobnie do modelu Druckera-Pragera wielkość dylatancji (ewolucji dodatnich objętościowych odkształceń plastycznych podczas ścinania plastycznego) można ograniczyć, wprowadzając maksymalny wskaźnik porowatości emax, dla którego oczekuje się osiągnięcia stanu krytycznego ψ = 0.
Parametry definiujące model materiałowy Soft soil podsumowano w poniższej tabeli.
Symbol | Jednostka | Opis | |
|
| Nachylenie linii pęcznienia | |
|
| Nachylenie linii normalnej konsolidacji izotropowej | |
|
| Maksymalny wskaźnik porowatości na wykresie | |
|
| Współczynnik Poisson'a | |
| [kPa] | Spójność efektywna | |
|
| Efektywny kąt tarcia wewnętrznego | |
|
| Kąt dylatancji | |
|
| Współczynnik parcia spoczynkowego gruntu normalnie skonsolidowanego | |
|
| Maksymalny wskaźnik porowatości do zakończenia dylatancji (przy ograniczeniu dylatacji) | |
|
| Wskaźnik prekonsolidacji | |
| [kPa] | Ciśnienie początkowe nadkładu | |
| [1/K] | Współczynnik rozszerzalności cieplnej (w przypadku uwzględnienia wpływu temperatury) | |
|
| Kąt tarcia wewnętrznego stanu krytycznego (nie zdefiniowany) | |
| [kPa] | Ciśnienie prekonsolidacji |
(nie zdefiniowane)Podobnie do modelu Zmodyfikowanego Cam-clay moduł sprężystości Younga nie jest wprowadzany bezpośrednio, ale raczej wyznaczany na podstawie modułu objętościowego Ks według
Jasne jest, że ewolucja sztywności, jak w przypadku modelu Zmodyfikowanego Cam-clay, zależy od średniego naprężenia efektywnego σm. Ustawienie początkowych wartości ciśnienia prekonsolidacji pcin, modułu objętościowego Ksin oraz początkowego wskaźnika porowatości 
jest opisane szczegółowo w prezentacji modelu Zmodyfikowanego Cam-clay. Jest to ściśle związane z wyborem kroku obciążenia początkowego, który wymaga bardzo niskich wartości naprężenia początkowego, aby były wystarczająco małe. W celu przyspieszenia zbieżności, przydatne wydaje się wykorzystanie minimalnej liczby iteracji dla pojedynczego kroku obciążenia. Wpływ wielkości kroku obciążenia początkowego na rozwój naprężeń i odkształceń jest szczegółowo opisany tutaj.
W przeciwieństwie do innych modeli typu Mohra-Coulomba, początkowy wskaźnik porowatości ein, który odpowiada stanowi gruntu na koniec pierwszej fazy obliczeń (naprężenie geostatyczne), nie jest wprowadzany, lecz wyznaczany obliczeniowo na podstawie wprowadzonej początkowej wartości wskaźnika porowatości e0 i bieżącego stanu naprężenia. Porównaj także opis modelu Zmodyfikowany Cam-clay.
Model pozwala na korektę początkowej wartości ciśnienia prekonsolidacji pc w zależności od oczekiwanego stopnia prekonsolidacji za pomocą parametrów 
i 
. Szczegółowe informacje można znaleźć tutaj. Należy pamiętać, że opcja ta jest dostępna tylko, gdy w ustawieniach wybrana jest opcja wyznaczania początkowego naprężenia geostatycznego za pomocą procedury K0.
W przypadku, gdy w analizie wymagane są warunki bez odpływu można procedować wyłącznie za pomocą Typu (1): analiza w naprężeniach efektywnych (cef, φe).
Model Soft soil umożliwia także wykonywanie analizy stateczności. Opcja ta jest jednak dostępna tylko podczas uruchamiania analizy stateczności w obrębie danej fazy budowy. W takim przypadku compression cap jest wyłączana. W związku z tym, tylko powierzchnia plastyczności w ścinaniu może stać się aktywna. Zadanie rozwiązuje się poprzez stopniową redukcję maksymalnych wartości parametrów wytrzymałości na ścinanie c, φ w sposób analogiczny jak podano w opisie modelu Druckera-Pragera.
W niniejszym artykule przedstawiono funkcjonowanie modelu w ramach prostych badań laboratoryjnych, w tym badanie porównawcze z modelem Zmodyfikowanym Cam-clay oraz wpływ wielkości początkowego kroku obciążenia.
Implementacja modelu materiałowego Soft Soil w programie GEO5 MES jest szczegółowo opisana w podręczniku teoretycznym.
Literatura:
[1] R.B.J. Brinkgreve, Geomaterial Models and Numerical Analysis of Softening, PhD thesis, Technische Universiteit Delft, 1994. Available at https://repository.tudelft.nl/record/uuid:6738de62-4dde-45b0-b3bd-3635504767c2.