Online Hilfe

Mohr-Coulomb (MC)

Biorąc pod uwagę fakt, że tradycyjna mechanika gruntów, a częściowo również mechanika skał, opiera się na tym modelu, model Mohra-Coulomba stanowi jeden z najczęściej stosowanych modeli materiałowych w praktyce inżynierskiej. W programie GEO5 MES odpowiadająca mu powierzchnia plastyczności jest definiowana za pomocą trzech funkcji granicznych, które w przestrzeni naprężeń głównych przedstawiane są jako nieregularny sześciokąt. Podobnie do modelu Druckera-Pragera powierzchnia plastyczności zależy od średniego naprężenia efektywnego σ_m^eff. Z projekcji powierzchni plastyczności f^{MC na} płaszczyznę dewiatorową oczywiste jest, że poszczególne krawędzie przecinają się w punkcie trójosiowego wydłużenia θ = - 30° i trójosiowego ściskania θ = 30°. Ponieważ powierzchnia plastyczności zależy również od kąta Lode'a θ, model jest w stanie zapewnić prognozy, które są bardziej zgodne z rzeczywistym zachowaniem gruntu w porównaniu do modelu Druckera-Pragera.

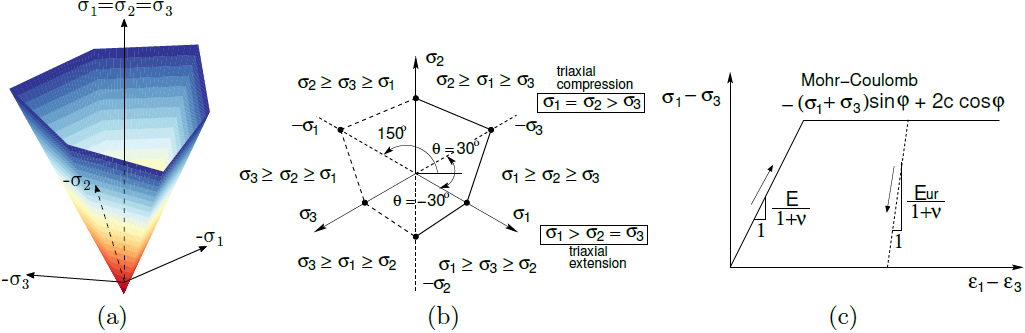a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) projekcja na płaszczyznę dewiatorową, c) prawo naprężenia-odkształcenia

Wykres naprężenia-odkształcenia sugeruje również, że model Mohra-Coulomba, podobnie jak zmodyfikowany model sprężysty, umożliwia modelowanie różnej reakcji gruntu przy obciążeniu pierwotnym oraz późniejszym odciążeniu i dociążeniu poprzez wprowadzenie modułu odciążenie/dociążenie E_ur.

Podobnie jak model Druckera-Pragera, model Mohra-Coulomba umożliwia uwzględnienie dylatancji gruntu (rozwój dodatnich objętościowych odkształceń plastycznych podczas ścinania plastycznego).

Analogiczne jest również rozwiązanie danego zadania w warunkach z odpływem lub bez odpływu. Więcej informacji, w tym listę wymaganych parametrów materiałowych, można znaleźć w opisie modelu Druckera-Pragera.

Szereg przykładów ilustrujących, porównujących prognozy numeryczne z rzeczywistym zachowaniem gruntu na podstawie prostych badań laboratoryjnych, można znaleźć tutaj. Przykład modelowania warunków bez odpływu znajduje się tutaj. Więcej szczegółów opisujących implementację warunków z odpływem i bez odpływu znajduje się w podręczniku teoretycznym.

W przeciwieństwie do modelu Druckera-Pragera, model Mohra-Coulomba, podobnie do modelu Hoeka-Browna, umożliwia ograniczenie wytrzymałości na rozciąganie, albo poprzez bezpośrednie zdefiniowanie wytrzymałości na rozciąganie σ_t < ccotφ, gdzie c, φ parametrami wytrzymałości na rozciąganie gruntu, lub poprzez wprowadzenie współczynnika redukcji wytrzymałości na rozciąganie TsRF. W tym przypadku uzyskuje się: . Zmniejszenie wytrzymałości na rozciąganie jest sterowane numerycznie przez powierzchnię plastyczności Rankina f^R. Graficzną reprezentację tego zjawiska przedstawiono na poniższym rysunku.

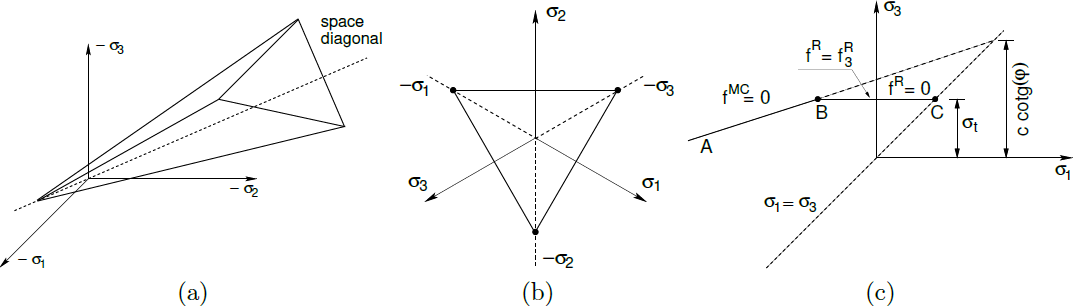a) powierzchnia plastyczności w przestrzeni naprężeń głównych, b) projekcja na płaszczyznę dewiatorową, c) projekcja powierzchni plastyczności Mohra-Coulomba i Rankina na płaszczyznę σ1 - σ3

Model Mohra-Coulomba, podobnie jak model Druckera-Pragera, pozwala na wykonywanie analiz stateczności. Można wykonać zarówno standardową analizę stateczności zbocza jak i analizę stateczności w obrębie danej fazy budowy. W obydwu przypadkach zadanie to rozwiązuje się poprzez stopniową redukcję parametrów wytrzymałości na ścinanie c, φ poprzez wprowadzenie parametru redukcji ζ takiego, że:

gdzie c, φ są właściwymi, rzeczywistymi parametrami wytrzymałościowymi, a c_d, φ_d parametrami zredukowanymi. Współczynnik stateczności FS wyznaczany jest następująco:

W podobny sposób redukowany jest kąt dylatancji ψ, pod warunkiem, że ψ ≠ 0.Implementację modelu materiałowego Druckera-Pragera do programu GEO5 MES opisano szczegółowo w podręczniku teoretycznym.