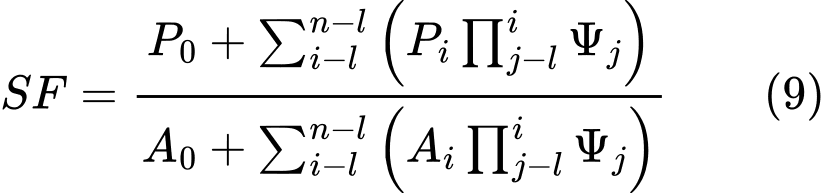Online Hilfe

ITF Method (Imbalance Thrust Force Method)

The ITF method is a limit state method. It builds upon the equation of equilibrium of forces acting on individual blocks and does not consider the moment equation of equilibrium. The bases of the method and adopted assumptions are evident from the following figure.

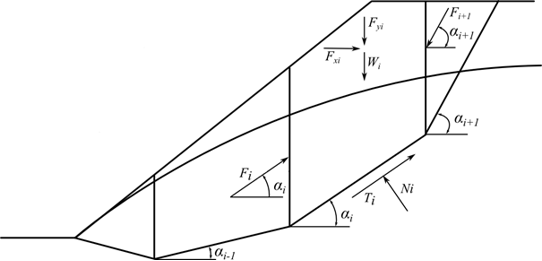Fig. 1 Forces acting on a block - ITF Method

Consider the following assumptions concerning the forces acting on the block:

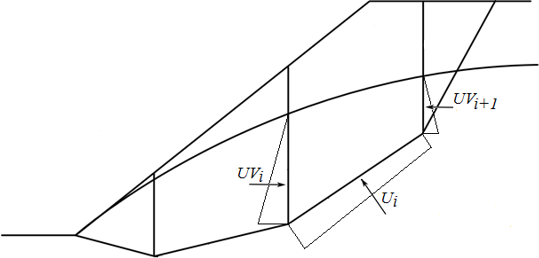Fig. 2 Scheme of pore pressure action on the block

The forces UV_i and UV_i+1 are included in the horizontal forces Fx_i.

The force equation of equilibrium in the direction normal to the segment of the slip surface provides:

The forces on the segment of a slip surface are related by

The force equation of equilibrium in the direction of the i^th segment of the slip surface (given by angle α_i) yields the force F_i acting between blocks in the form:

Introducing Eqs.(1) and (2) into Eq. (3) provides:

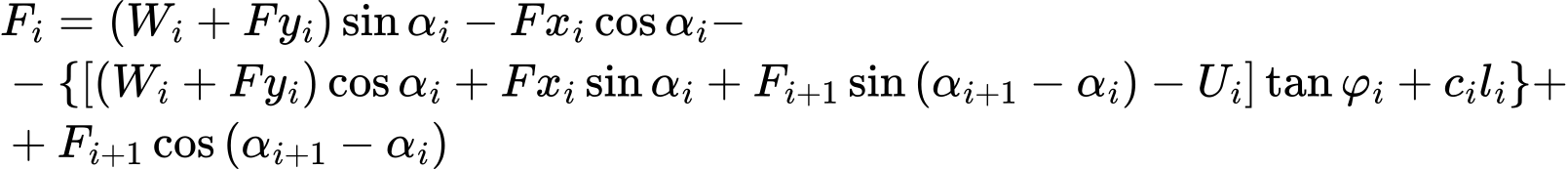
and after some formal algebra, we arrive at the resulting form of the equation of equilibrium as:

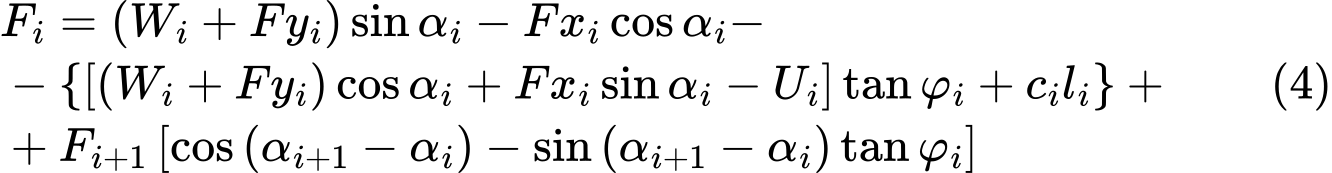
The equilibrium condition will be fulfilled by introducing the factor of safety SFS into the analysis such that the strength parameters of a given soil c and tanφ are divided by this value. Eq. (4) then becomes

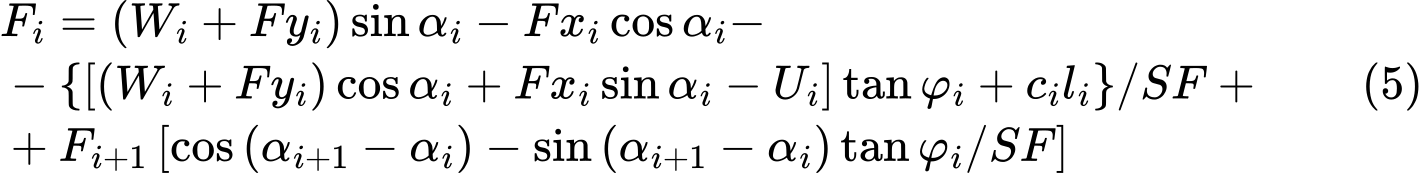
Eq. (5) then gives the searched factor of safety SF through the process of iteration. This process proceeds such that the force F_n equal to 0 kN is applied at the highest (end) point of the slip surface. The forces F_i acting in between blocks are determined for a given value of the factor of safety SF from Eq. (5). This step is repeated for various values of SF until we find such SF for which the force F₀ at the slope base becomes equal to 0 kN. No tension is assumed along the slip surface. If the equilibrium condition requires the value of normal force N_i being negative, which means that the soil is loaded in tension, then the value of this force is set equal to zero in the next iteration step and the shear force T_i acting on a given segment is determined based on the soil cohesion only.

The ITF method is quite sensitive with respect to the shape of the slip surface. In case the slip surface contains sharp segment discontinuities the resulting factor of safety is generally larger when compares to reality. It is recommended that the slope difference between adjacent segments of the slip surface be less than 10°. This is checked automatically by the program and if the slope difference is found greater the programs prompt a warning that the results might be overestimated. This is usually not the problem of a circular slip surface but should be kept in mind in case of polygonal slip surfaces.

ITF Method - explicit solution

The explicit solution of the ITF method assumes a different way of introducing the factor of safety into the analysis. The mathematical solution then does not require iterations and the resulting factor of safety is calculated directly in one step. With this approach, the resulting factor of safety is typically higher which may the solution totally devalued, particularly in cases concerning polygonal slip surfaces with large slope differences of adjacent segments.

The solution exploits Eq. (4) to which the factor of safety SF is introduced such that it multiplies the active components of forces, i.e. the components acting in the sliding direction. The equilibrium condition then becomes :

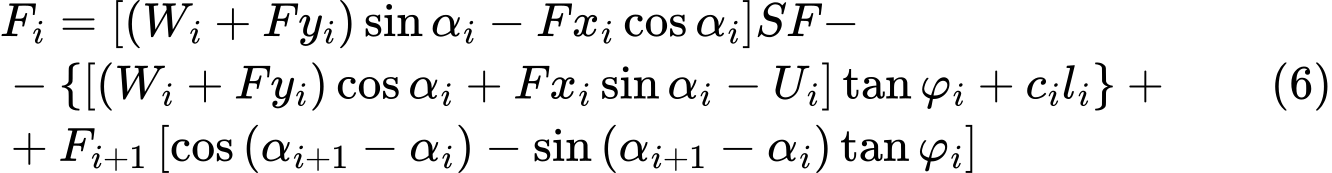
For lucidity, we introduce the component of active forces as:

and next to the component of passive forces as:

and an auxiliary function:

Eq. (6) can then be written in more compact form as:

The next step assumes the known force F_n=0 to provide expressions of forces between blocks F in the form:

Etc….

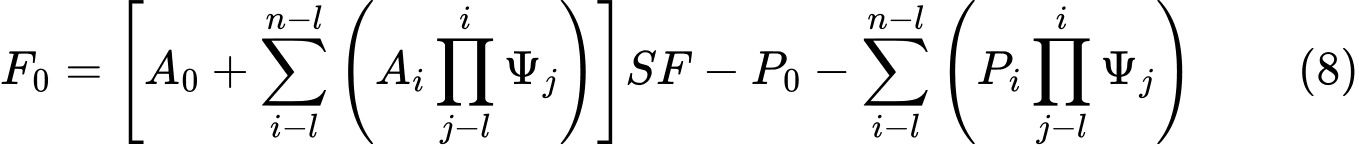
And since the force on the bottom origin of the slip surface should be equal to 0 kN, we get the final form of the factor of safety SF as: